L i s t D i r e c t o r y : P r o b l e m D e s c r i p t i o n
-
Procedure
Read directory trees is a fundamental task in system administration, integrated in a variety of treatments. Programs / snippets - available in the internet - resort to a few algorithms, which in fact solve a general problem: search a hierarchical graph. We'd rather understand them thoroughly, in order to implement - or select - robust programs.
Project List_Dir complies with the programing guide lines previously discussed. In the current context, they summarize as follows.
- Define the task as exactly as possible, before writing a single line of code. More accurate than natural languages, mathematical definitions shall point at difficulties and provide clues toward an algorithmic resolution.
- Link the mathematical objects defined to functions/procedures available in operating systems or Perl libraries.
- Discuss and propose implementations. Ideally, codes should be so modular that alternative algorithms can easily be integrated.
Project List_Dir is the first step toward "advanced" projects like "count lines of code" (CLC) or "back up data" (BUD) to be presented later.
-
Definitions
The task will be equated to resolving operator List_Dir({ElemName}) taking file system element {ElemName} as an argument. What this syntax actually means, will become clear as the analysis progresses.- Definition 1: Directories are oriented graphs
Let us reflect users experiences without attempting to establish correlations with known file systems at first. A directory can be seen as a hierarchical graph connecting elements of type directory (DirName) or file (FilName) (Fig. Directory Structure).
- Files - represented as rectangles - are containing data meaningful to users.
- Directories - represented as circles - are only a mean to retrieve files.
A biological analog is the branches of a tree - the root directory being the trunk. Each branch decomposes till the path ends after a finite number of bifurcations - mostly at leaves, the atomic elements, similar to files.
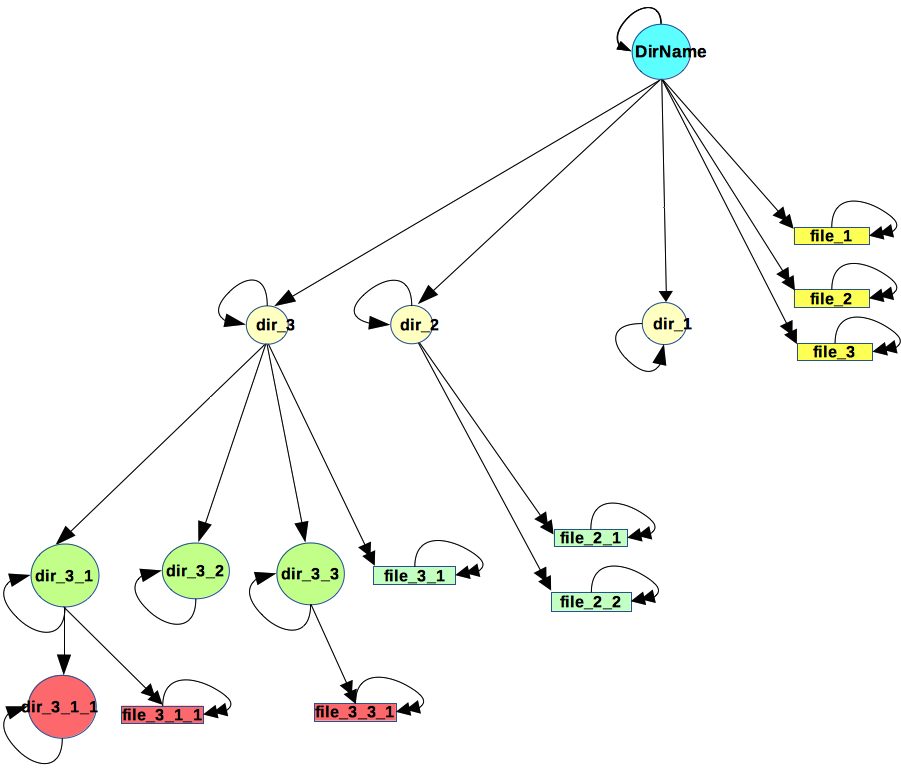
Fig.: Directory structure - stretching over 4 levels: 0 (the root level), 1 (yellow), 2 (green), 3 (salmon)Note about links:
 Soft (symbolic) links
are files and will be treated like any other file - ignoring what they point out.
Soft (symbolic) links
are files and will be treated like any other file - ignoring what they point out.
-
 Hard links
- when available - operates
at a deeper software layer level than user interfaces to file systems. For most users those links cannot be set apart from
the data they point at. Therefore, it is legitimate to consider them not being part of the actual content of the directory where they are stored.
Hard links
- when available - operates
at a deeper software layer level than user interfaces to file systems. For most users those links cannot be set apart from
the data they point at. Therefore, it is legitimate to consider them not being part of the actual content of the directory where they are stored.
-
Definition 2:
 Relation
owns_directly
Relation
owns_directly
In fig. 'Directory Structure'
- Nodes represent the file system elements contained: files, directories.
-
Edges express the owns_directly-relation
e.g. DirName owns_directly file_1_1 also expressed {file_1_1} ⊂ owns_directly(DirName) (In words: {file_1_1} is part of image of DirName in relation owns_directly.)
owns_directly is obviously not a
 function:
It can return a set of elements {elem1, .. elemn} (In words: A directory can own several elements). Also following properties are valid:
function:
It can return a set of elements {elem1, .. elemn} (In words: A directory can own several elements). Also following properties are valid:
-
owns_directly will be assumed
 reflexive:
It always returns the argument itself: ∀ elem: elem owns_directly elem.
reflexive:
It always returns the argument itself: ∀ elem: elem owns_directly elem.
If the argument is a directory, it possibly returns files ({F}; F/file) and directories ({D}; D/Directory) e.g.
- owns_directly(DirName) = {file_1_1,...,file_1_3}∪{DirName, dir_1_1,..., dir_1_3} (path continues)
- owns_directly(dir_1_2) = {file_2_2, file_2_22}∪{dir_1_2} (path ends)
- owns_directly(dir_1_1) = {dir_1_1} (path ends)
If (A,B) directories and A ≠ B and A owns_directly B, then B is a sub- or child- directory of A, and A is a parent-directory of B
e.g. dir_1_1 is a subdirectory of DirName . If the argument of owns_directly is a file, owns_directly only returns the file itself (path ends)
e.g. file_2_31 owns_directly file_2_31owns_directly is
 antisymmetric,
antisymmetric,
∀ A, B; (A owns_directly B) and (B owns_directly A) → (A = B).
In words: A directory is never parent of its parent directory - no multi-elemental loops in the graph.owns_directly is "kind of"
 injective
(injectivity is actually only defined for
injective
(injectivity is actually only defined for  function)
function)
∀ A, B, C; ( (A ≠ B) and (A owns_directly B) ) and ( (C ≠ B) and (C owns_directly B) ) → (A = C).
In words: A directory is never owned directly by two different parent-directories.
Relation is_owned_directly_by can be defined as owns_directly-1: if A owns_directly B, then B is_owned_directly_by A. As a matter of fact is_owned_directly_by - because of the "kind of" injectivity - is simpler to manipulate than owns_directly, but of no practical use. -
Definition 3:
 Relation
owns
Relation
owns
is derived from owns_directly as follows: A owns B, if and only if :- A owns_directly B or
- [eq. IV 2-A] ∃ C; A owns C ∧ C owns_directly B
In words: A owns B, if and only if A directly owns B or if A owns a directory C that directly owns B.
Note:-
owns is nothing else than the completion of
owns_directly toward transitivity. Therefore, [eq. IV 2-A]
can be formulated more generally - and elegantly - by only stating owns-
 transitivity
transitivity
[eq. IV 2-B] ∀ A, if (∃ B; (A owns B)) ∧ (∃ C; (B owns C)) then A owns C.
In words: For all A, B, C, if A owns B and if B owns C then A owns C. - [eq. IV 2-A] and [eq. IV 2-B] are equivalent. [eq. IV 2-A] however may be closer to an algorithmic resolution.
Completion toward transitivity is realized through operator composition e.g.
(owns_directly∘owns_directly)({DirName}) = owns_directly2({DirName}) =
{file_1_1,file_1_2,file_1_3,file_2_31,file_2_21,file_2_22}∪{dir_1_1,dir_2_31,dir_2_32,dir_2_33}.Note:
Operator "Composition" is made possible because of a fundamental property of relations: distributivity
toward
distributivity
toward
 union of sets.
Relations do not only apply to single elements, but to sets of elements, whereat
image Relation({set_1}∪{set_2}) equates to
image Relation({set_1})∪Relation({set_2}).
union of sets.
Relations do not only apply to single elements, but to sets of elements, whereat
image Relation({set_1}∪{set_2}) equates to
image Relation({set_1})∪Relation({set_2}).
Derived properties:
Because of owns-properties - reflexivity, anti-symmetry, transitivity -, a file system is
 ordered
(not completely but partially ordered though) - which, using composition, means
ordered
(not completely but partially ordered though) - which, using composition, means
∀ A, B ; owns(A) ⊃ {B}, ∃ n ∈ N : owns_directlyn (A) ⊃ {B}
In words: Every element B owned by A, can be retrieved along at least one path.Because of owns_directly kind of injectivity, we can even state following:
∀ A, B ; owns(A) ⊃ {B}, ∃! (A1,..., An) /Dirn;
A owns_directly A1...An-1 owns_directly An owns_directly B .
In words: Every element B owned by A, can be retrieved along a unique path.
Starting from any file system element (called the root), we can calculate all images Imk iteratively (k integer):
- Im0 = {ElemName}
- Im1 = owns_directly({ElemName})
- Imk+1 = owns_directly({Imagek}) = owns_directlyk+1 (ElemName)
Each new composition resolves each element into its content - which equates to a progression along the content path. Since real systems are finite, owns(DirName) is a finite set. There is a finite number of paths and each path terminates. In mathematical terms:
∃ n (integer); ∀ k; k ≥ n: Imk[owns_directly(ElemName)] = Imn[owns_directly(ElemName)].
Let us call this k integer, k_owns. -
Definition 4: Back to List_Dir({DirName})
List_Dir(DirName) = Imk_owns owns_directly({ElemName})
After composing owns_directly({ElemName}) at least k_owns times, the obtained image contains all files and directories owned. In many cases, only files are of interest.
- Definition 1: Directories are oriented graphs
-
- Elementary Search Step
Operating systems implement commands to show directory contents:
-
In Unix (see also Unix Shell) command
 ls
(ls DirName) applies.
Option -R triggers recursive listing.
ls
(ls DirName) applies.
Option -R triggers recursive listing.
If the final objective is only to display contents, it suffices to run ls -l -R DirName - and parse its output, using grep
and
grep
and
 sed,
as shown e.g.
sed,
as shown e.g.  here.
here.
-
In Microsoft Windows (see also cmd.exe or command.com)
-
command
 dir
(dir DirName) shows the direct (next level) content of a directory.
dir
(dir DirName) shows the direct (next level) content of a directory.
-
command
 tree
(tree DirName) shows the entire content of a directory tree (all sub-levels).
tree
(tree DirName) shows the entire content of a directory tree (all sub-levels).
Like for Unix, if the sole objective is to display contents, the existing commands suffice, possibly parsed to control and/or filter the output. -
command
Perl offers function
Actually readdir prepends two "special" names. readdir DIRHANDLE,
which returns the content of directory referred to by DIRHANDLE
readdir DIRHANDLE,
which returns the content of directory referred to by DIRHANDLE
e.g. @dirElemNames = readdir DIRHANDLE stores in array @dirElemNames the content, file or directory names.- Name . representing the current library - referred to by DIRHANDLE
- Name .. representing its parent directory
Obviously commands ls, dir and Perl function readdir are the counterpart of relation owns_directly. They enable to go one step forward in the tree. After a finite number of compositions / iterations, all elements on all paths are identified.
-
- Overall Search Strategies
Which strategy is suitable to explore directory trees? Answers can be formulated along different perspectives, e.g. a theoretical point of view or the implementation point of view.
-
Theoretical considerations
There are plenty of theoretical researches about search algorithms. I will not discuss their premisses and results, even briefly - this would exceed by far the intended scope. For now, it will suffice to mention following pieces of information.
-
An introduction to
 tree-search
- also called "Tree Traversal" (Of interest are the antithetic search modes: depth- or breadth- first).
tree-search
- also called "Tree Traversal" (Of interest are the antithetic search modes: depth- or breadth- first).
-
Search directory trees pertains to a wider problem, 'Define Search Strategies', of which resolution,
enables implementing
 mathematical proof,
e.g. programs to proof theorems, to validate specifications, to define test cases.
An understanding of the general case may help define solutions more efficient than those to be discussed here.
mathematical proof,
e.g. programs to proof theorems, to validate specifications, to define test cases.
An understanding of the general case may help define solutions more efficient than those to be discussed here.
-
An introduction to
-
Implementation alternatives
-
Using recursion: The function implementing the one-step-search invokes itself.
sub DirList( ListOfContent_Old )
{
Find and treat first element in resolution stack
ListOfContent_New = ListOfContent_Old - {FirstElement};
If stack is empty, nothing to do.
if {FirstElement}={} then return ()
If FirstElement is a file, add it to result list and process the remaining unresolved content
return ( {firstElement}, DirList(ListOfContent_New) );
If FirstElement is a directory, process it first and then the remaining unresolved content
ListOfContentFirstElem = ResolveContentOfElem(FirstElement);
{SubFiles} = Files (ListOfContentFirstElem);
{SubDirs} = Dirs (ListOfContentFirstElem);
return ( {SubFiles}, DirList(SubDirs), DirList(ListOfContent_New) );
}
Remarks to tree-search by recursion:
- ListOfContent_Old contains the content to resolve as the current iteration starts.
- The first element in ListOfContent_Old is extracted and treated by function ResolveContentOfElem() that returns content ListOfContentFirstElem.
- ListOfContentFirstElem is then split into files (final element) and directories (which must be resolved anew).
- The next iteration invokes the function itself on the new unresolved contents. It terminates when no content is left to resolve.
Historically, I first dealt with recursive algorithms for exploration of directory trees. My results have been published List_Dir_1x Versions List_Dir_2x (not published yet) examine algorithms based on iteration loops.
-
Using loops: The tree-search function encapsulates the one-step-search within a loop (In procedural languages, the usual way to proceeed iterations).
sub DirList( ListOfContent_Old )
{
Initialize loop
Delta_ListOfContent = ListOfContent_Old;
Treatment goes on, as long as new content to resolve is detected
while ( Delta_ListOfContent != {} )
Go next path along the tree and collect content
ListOfContent_New = ResolveContentOfList(ListOfContent_Old)
Identify added content, if any
Delta_ListOfContent = ListOfContent_New - ListOfContent_Old;
Initialize next iteration
ListOfContent_Old = ListOfContent_New;
end of while;
Return extended list after complete resolution of all contents.
return (ListOfContent_New);
}
Remarks to tree-search by loops:
- ListOfContent_Old contains the list of elements to resolve.
- Function ResolveContentOfList() performs one resolution step and returns the next content to resolve: ListOfContent_New.
- Iteration terminates, when it does not add content:
-
-
- Elementary Search Step